The ability to generate high quality novel images has been the target of extensive research in the deep learning and computer vision field. Generative adversarial networks (GANs) showed us that we could implicitly learn the distribution of data and draw samples from this distribution; VAEs showed us how to explicitly map data to a (gaussian) distribution and learn the parameters of this distribution. However, we could only generate small blurry images - 64x64px; and when we got better at larger images, we still had diversity and quality problems and at very high computational cost.

Recently, there has been the introduction of diffusion models - models that learn a noising process (adding noise to some input across several steps until that input is indistinguishable from pure noise) and a denoising process that reverses the noising process (removes noise across several steps until a legit image is recovered). The name diffusion comes from a branch of physics (non-equilibrium thermodynamics) which describes how particles may move from areas of high concentration to lower concentration in order to achieve equilibrium. In practice, while diffusion models yield very high image quality, many challenges (slow sampling due to a large number of denoising steps etc) have had to be addressed to make this process usable in image generation - with landmark papers like , DDPM[^1], DDIM[^2] etc.

More recently latent diffusion models[^3] were introduced and address an important challeng with diffusion models - their memory requirements. They achieve this by proposing we apply the noising and denoising process in latent space (instead of raw image/pixel space) and then map this latent space back to the image space. This dramatically reduces the memory requirements for running diffusion models, hence the competitive results we have seen recently on consumer GPUs.

But what does this whole noising/denoising process look like in practice? Let's dig in.

Components of a Latent Diffusion Model

To implement a diffusion model we want to train a model capable of performing the noising and denoising steps mentioned above. At inference time (generating new images), we perform the denoising step - we start from some noise vector, iteratively denoise it to get a clear image. In addition to this, we also want to assert some form of control or conditioning over content of the final clear image - we want to be able to describe the type of image we want (e.g.free form text) or as seen in an image, or both.

The latent diffusion model has several components that help us achieve this.

• VAE: A traditional variational autoencoder that learns to map data to a parameterized distribution. It consists of an encoder that maps an image to a (low dimension) latent space representation and a decoder that reconstructs the image from this latent representation (by sampling from the learned distribution).
• Unet: This model (also an encoder decoder architecture) is used to learn the noising/denoising steps. E.g. in the denoising loop, it takes in some noise, time step information and some conditioning signal (e.g., representation of some text description), and predicts noise residuals which can be applied in denoising.
• Scheduler: Scheduler algorightm that helps us control the amount of noise added to the input image at each step of the noising process.
• Text Encoder: A model that yields a representation of the text signal used to condition the denoising process. Typically, this representation should be aware of both the text and image domains, making CLIP models a good choice for this task.

This general setup can be rigged to enable nice applications such as:

• Image to image generation : Here, rather than starting from random noise as input to the Unet sampling loop, we start from the latent space representation of the image. We can recover this using a simple vae.encode() call.
• Inpainting: Here, we start from the latent space representation of the image as above, but we mask out some part of the image (set its value to 0 or 1).

In general, I find that thinking of a diffusion model in terms of these sets of components can inspire a set of interesting questions e.g., Are there more efficient conditional signals beyond text? Can we apply embedding arithmetic in modifying conditioning signals (e.g. take some image embedding, subtract some text embedding and use the result as conditional signal?)

The Denoising Process Implementation with HuggingFace Diffusers

for i, t in tqdm(enumerate(self.scheduler.timesteps[t_start:])):
  # expand the latents if we are doing classifier free guidance
  latent_model_input = (
      torch.cat([latents] * 2) if do_classifier_free_guidance else latents
  )
  if isinstance(self.scheduler, LMSDiscreteScheduler):
      sigma = self.scheduler.sigmas[i]
      latent_model_input = latent_model_input / ((sigma**2 + 1) ** 0.5)

  # predict the noise residual
  noise_pred = self.unet(
      latent_model_input, t, encoder_hidden_states=text_embeddings
  )["sample"]

  # perform guidance
  if do_classifier_free_guidance:
      noise_pred_uncond, noise_pred_text = noise_pred.chunk(2)
      noise_pred = noise_pred_uncond + guidance_scale * (
          noise_pred_text - noise_pred_uncond
      )

  # compute the previous noisy sample x_t -> x_t-1
  if isinstance(self.scheduler, LMSDiscreteScheduler):
      latents = self.scheduler.step(
          noise_pred, i, latents, **extra_step_kwargs
      )["prev_sample"]
  else:
      latents = self.scheduler.step(
          noise_pred, t, latents, **extra_step_kwargs
      )["prev_sample"]
  if return_intermediates:
      decoded_image = decode_image(latents, self.vae)
      intermediate_images.append(self.numpy_to_pil(decoded_image))

In the snippet above, the most important line is the self.unet call where we predict the noise residuals, followed by applying guidance/conditioning from the text embeddings in determining the latent space representation of the image at the current time step. Given this, we can then use this latent presentation to sample from the vae and save the resulting intermediate images.

Further Reading

There are few great resources to learn more about diffusion models:

• What are Diffusion Models? by Lilian Weng. Discusses the mathematics behind diffusion models and how they work.
• Stable Diffusion with 🧨 Diffusers by Huggingface team. Discusses the implementation of the stable diffusion model in the Diffusers library.
• High-Resolution Image Synthesis With Latent Diffusion Models. The original paper introducing latent diffusion models.

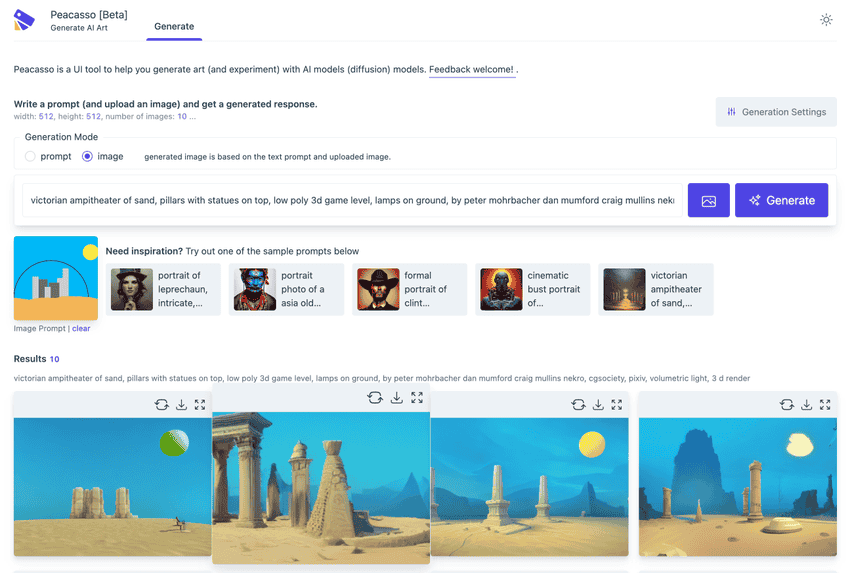
Introducing Peacasso

The simplicity and sheer quality of images from latent diffusion models are quite mesmerizing. As these models become even more accessible (reduced model size, faster inference), we can expect to see more and more applications of these models in the wild.

To help improve the user experience with these models, I have been working on Peacasso - UI interface for experimenting with multimodal (text, image) models (stable diffusion). Beta testers welcome!

References

[1]: Ho, Jonathan, Ajay Jain, and Pieter Abbeel. "Denoising diffusion probabilistic models." Advances in Neural Information Processing Systems 33 (2020): 6840-6851.

[2]: Song, Jiaming, Chenlin Meng, and Stefano Ermon. "Denoising diffusion implicit models." arXiv preprint arXiv:2010.02502 (2020).

[3]: Rombach, Robin, et al. "High-resolution image synthesis with latent diffusion models." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022.